Тема: Границя функції в точці. Задачі, що приводять до поняття похідної.
Мета: сформувати поняття приросту аргументу та приросту функції, розглянути задачі, що приводять до поняття похідної.
Шановні 10-класники!
На мою електронну скриньку почали надходити "перші ластівки". Що тішить і радує. Хтось всі завдання виконав, хтось лише контрольну роботу, а решту завдань не помітив, а хтось ще і не починав.
Кожний вид роботи буде оцінений.
Чекаю активних рухів від решти!
Велике прохання до вас - поставитися з розумінням до того, що ваші звіти мають приходити у визначений час і на електронну скриньку вчителя irinazabiyaka68@ukr.net.
На вайбер приймаю роботи тих учнів, які з технічних причин не можуть надіслати зі своєї електронної скриньки, бо маю телефон з обмеженою кількістю пам'яті.
Дякую за розуміння!
За вікном весна, а у нас карантин...
І щоб зберегти здоров'я і життя своє та рідних вам людей ми змушені і БУДЕМО залишатися ВДОМА!
Продовжуємо навчатися дистанційно!
Предмет, який ми вивчаємо, має назву "Алгебра і початки аналізу". Тут йдеться про початки одного з розділів математики - математичного аналізу.
Цей розділ об'єднує диференціальне й інтегральне числення.
Диференціальне числення вивчає означення, властивості та застосування похідних функцій. А сам процес знаходження похідної функції називають диференціюванням.
Інтегральне числення - це вивчення двох взаємопов'язаних понять - невизначеного та визначеного інтегралів.
Сьогодні ми починаємо вивчати один із розділів математичного аналізу - диференціальне числення.
Ми дізнаємося, що називається похідною функції, навчимося знаходити похідні функцій; дізнаємося як похідні функцій застосовують до розв'язування практичних задач.
1. Розглянемо поняття границі функції на нескінченності та границі функції в точці:
2. Розглянемо функцію і дамо означення, що називають приростом аргументу та приростом функції:
3. Розглянемо приклад: Знайдіть приріст функції f у точці x0 при вказаному прирості аргументу dx:
1) f(х)=3x-2, х0=-1, dx=0,3;
Розв'язання:
Приріст функції обчислюємо за формулою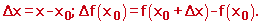 Виконаємо обчислення для заданої функції
Виконаємо обчислення для заданої функції
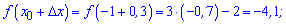
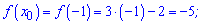
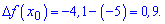
Отримали, що приріст рівний 0,9.
Приріст функції обчислюємо за формулою
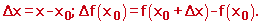 Виконаємо обчислення для заданої функції
Виконаємо обчислення для заданої функції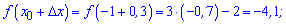
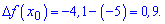
Отримали, що приріст рівний 0,9.
2) f(x)=sin(х), х0=0, dх=Pі/6.
Розв'язання:
Виконаємо пряму підстановку в формулу приросту функції
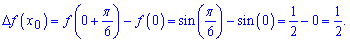
4. Перегляньте відео. У ньому розглядаються задачі, які приводять до поняття похідної:Виконаємо пряму підстановку в формулу приросту функції
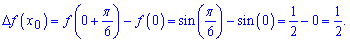
- задача про миттєву швидкість;
- задача про дотичну до графіка.
Отже, переглянувши пояснення вчителя, можна зробити такі висновки:
1)
2) кутовий коефіцієнт k дотичної графіка функції f у точці з абсцисою х0 визначають за допомогою формули:
5. Розглянемо задачу № 18.7 за підручником с. 108.
Матеріальна точка рухається по координатній прямій за законом s(t) = 2t^2 + 3 (переміщення вимірюють у метрах, час - у секундах). Знайдіть миттєву швидкість матеріальної точки в момент часу t0 = 2 с.
Розв'язання:
Відповідь: 8 м/c.
6. Домашнє завдання:
- опрацювати урок і за підручником прочитати п. 18, с. 103-107, виписати в зошит і вивчити :
- означення приросту аргументу, приросту функції,
- формулу миттєвої швидкості та формулу кутового коефіцієнта дотичної до графіка функції;
- виконати №№ 18.2, 18.6;
- надіслати звіт вчителю на електронну скриньку не пізніше 9 години 26 березня.
Успіхів у здобуванні освіти!
До зустрічі на наступному занятті!











Немає коментарів:
Дописати коментар