11 клас геометрія, заняття 8

Тема: Зрізаний конус та його поверхня.

Мета: узагальнити та систематизувати знання, уміння та навички з даної теми.

Шановні 11-класники!

З метою повторення даної теми перегляньте урок:

Розглянемо задачу, що була в ЗНО минулих років (запишіть у зошит):

Задача. Радіуси основ зрізаного конуса дорівнюють 7 см і 15 см, а його твірна – 10 см. Знайти висоту конуса.

Розв'язання: Маємо зрізаний конус, основами якої є концентричні кола з центрами O та O1, де O1=H – висота зрізаного конуса і радіусами AO=15 см, A1O1=7 см відповідно.

Оскільки висота OO1 перпендикулярна до площин основи зрізаного конуса, то вона перпендикулярна до кожної прямої, що лежить в цих площинах, тому O1⊥AO та OO1⊥A1O1.

Звідси слідує, що чотирикутник AA1O1O – прямокутна трапеція, висота OO1 якої є висотою зрізаного конуса.

Проведемо відрізок A1K=O1O, тобто A1K⊥A.

Тут маємо KO=A1O1=7см, тоді AK=AO-KO=15-7=8 см.

Розглянемо прямокутний трикутник AKA1 (∠AKA1=90), у якого AA1=10 см – гіпотенуза (довжина твірної конуса) та AK=8 см – катет.

За теоремою Піфагора знайдемо катет A1K=O1O – висоту зрізаного конуса:

A1K2=AA12-AK2, звідси

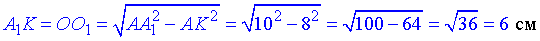
Відповідь: 6 см.

Домашнє завдання: Розв"яжіть задачу:

Відношення площі основи конуса до площі осьового перерізу дорівнює π. Знайти кут нахилу твірної до основи (в градусах).

А) 15;      Б) 30;      В) 45;   Г) 60;   Д) 75.

Свої звіти надсилати на електронну скриньку вчителя.

Ви все зможете! Вірю в вас!

Далі буде...